Name: rebecca

Who is asking: Other
Level: All

Question:
You have a unit circle, radius=1. Around the outside of the circle are the letters A thru F, evenly spaced. (all 60 degrees apart). The center of the circle is O. There is an arc connecting C with E. This arc has a midpoint, G. If we extend the arc CGE to make another circle, point A is the center of this new circle. The area between arc CGE and arc CDE (of the original circle) is shaded. My question is, what is the number of square units of area in the shaded region?

I am an education major at Penn State. My assignment is to write a lesson plan to teach others to solve this problem, only I cannot figure out how to do it. If you could offer any assistance as to how I do this. I would greatly appreciate it. The official statement of the problem given to me is " Points A,B,C,D,E,F are equally spaced on a unit circle. Arc CGE has a center A. Find the number of square units of area in the shaded region.

First, I would suggest creating an accurate sketch, using something like The Geometer's Sketchpad or Cabri. (I did!)

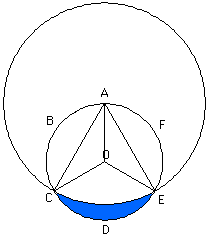The key to making the sketch is that the second circle is just created as a circle center A radius AC. This circle passes through E. Now we can find the desired area by calculuating three areas: (a) the area of the sector ACE in the larger circle; (b) the areas of the two triangles ACO and A0E; (c) the area of the sector 0CE in the smaller circle. The final answer is found by substraction: (b)+(c) - (a). The area of a sector is 1/2 r^2 theta where theta is measured in radians so the areas of the two sectors can be found using: (a) the angle is Pi/3 radians and the radius is root 3; and (c) the angle is 2 Pi/3 radians and the radius is 1. For (b) we have two triangles with base root three and height 1/2. Walter