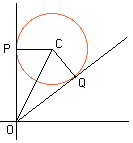
Question:
Two tangents are drawn from the origin to the circle (x)(x)+(y)(y)-4x-6y+9=0. If the angle between the tangents is m, fine the value of tan(m).

P.S. (x)(x)=square x

I am going to write (x)(x) as x^2.

Completing the squares in both x and y the equation of the circle can be written

x^2 -4 x + 4 + y^2 -6 y + 9 = 9, or

(x-2)^2 + (y-3)^2 = 9. Thus the circle has center (2,3) and radius 2.

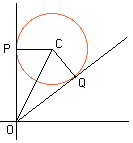Thus one of the tangent lines is the y-axis. Let P be the point on the y-axis where the circle is tangent to it, Q the point where the second tangent meets the circle and C the center of the circle. Since CPO and OQC are right angles and |PC| = |CQ| = 2 the triangles CPO and QCO are congruent. Thus angle POC is (1/2)m and therefore tan(m/2) = 2/3. The double angle formula for the tangent now gives tan(m) = 12/5.

Cheers,
Harley