Date: Sat, 2 Nov 1996 10:32:30 -0500
Subject: PRECALCULUS

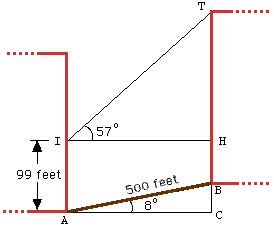
"IRENE" IS TO DETERMINE THE # OF FLOORS IN A HOTEL 500 FEET UP THE STREET. IRENE IS ON THE 10TH FLOOR OF AN OFFICE BUILDING AND CAN MEASURE THE ANGLE OF ELEVATION TO THE TOP OF THE HOTEL, 57 DEGREES. HER VIEW OF THE ENTIRE BUILDING IS OBSTRUCTED. IF THE STREET RISES AT AN ANGLE 8 DEGREES FROM THE OFFICE BUILDING TO THE HOTEL AND THE AVERAGE DISTANCE BETWEEN FLOORS IS 11 FEET, HOW MANY FLOORS ARE ON THE HOTEL? (I BELIEVE WE PROBABLY HAVE FUNCTIONS OF TWO TRIANGLES TO DETERMINE -- FIRST, THE TRIANGLE CREATED WITH THE 8 DEGREE ELEVATION (DISTANCE OF "Y" TO BE SUBTRACTED FROM ANSWER OF HEIGHT OF SECOND TRIANGLE). I AM USING TANGENT FORMULAS (Y/X OR OPPOSITE/ADJACENT) TO DETERMINE, BUT COME UP WITH FINAL ANSWER OF 707.22 FEET AS HEIGHT OF HOTEL. I DON'T THINK THIS IS CORRECT AND NEED HELP FIGURING OUT WHERE I'VE GONE WRONG. ANY HELP WOULD BE APPRECIATED. THANKS.

It sounds like you have the proper approach to this problem, but I don't get the same answer that you do.

In the diagram sin(8 deg) = BC/AB and cos(8 deg) = CA/AB. Since AB=500 ft., BC = 69.59 ft and CA = 495.13 ft.

Irene is standing at I and I have taken the angle of elevation to be measured from the floor of the tenth floor. Here tan(57 deg) = TH/HI and HI = CA = 495.13 ft so TH = 762.43 ft. Hence the height of the building is TB = TH + HC - BC = 792.84 ft. So the building must have 72 floors.

Cheers
Penny