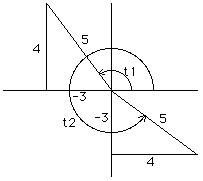
In the fourth quadrant the angle t2 has sin t2 = -3/5 and cos t2 = 4/5 so cot t2 = -4/3.
Date: Wed, 11 Dec 1996 23:09:24 -0600 (CST) Subject: Trig problemWho is asking: Student
Question:
sin t + cos t = 1/5
Find ALL exact values of cot t, given the original equation.
Please give me a hand with this, and explain it VERY well
If the fraction 1/5 makes you think of the 3-4-5 triangle then you can spot two solutions.
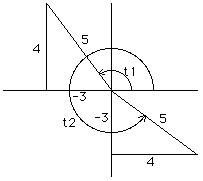
|
In the second quadrant the angle t1 has sin t1 = 4/5 and cos t1 = -3/5 so cot
t1 = -3/4. In the fourth quadrant the angle t2 has sin t2 = -3/5 and cos t2 = 4/5 so cot t2 = -4/3. |
|
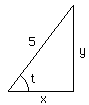
Thus if t is an angle that solves your problem then x/5 + y/5 = 1/5 and x^2 + y^2 = 25. Since the graph of the first equation is a straight line and the graph of the second equation is a circle there can be at most two points of intersection. Alternatively you can solve the two equations. The first gives y = 1 - x. Substituting into the second and simplifying gives x^2 - x - 12 = 0 or (x-4)(x+3)=0. Thus x = -3 or x = 4 giving the 3-4-5 triangle mentioned above. |
To return to the previous page use your browser's back button.