Date: Wed, 18 Dec 1996 13:52:58 -0600 (CST) 
Subject: Geometry

Question:
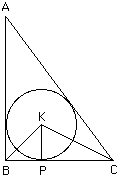
Given that Triangle ABC is a right triangle and Circle O is inscribed in it find the radius of Circle O, totally in terms of a, b, and c.

If K is the center of the circle, r is its radius and P is the point where the circle touches the side BC then BC is perpendicular to KP so the area of the triangle KBC is (1/2)*a*r. Making the same observation for each of the other two sides you can see that the area of the triangle ABC is (1/2)*a*r + (1/2)*b*r + (1/2)*c*r. Since angle ABC is a right angle the area of the triangle ABC can also be written (1/2)*a*b. Thus (1/2)*a*b = (1/2)*a*r + (1/2)*b*r + (1/2)*c*r or r = a*b/(a+b+c).

Cheers
Penny