Who is asking: Student
Level: Secondary

Question:
The following towns are placed on a coordinate system. Ajax at (-x,z), Dilltown at (-10,0), Canton at (0,0) and Beverly at (0,10). The roads from Beverly to Canton and from Canton to Dilltown are perpendiculat to each other and are each 10 miles in length. A car traveling at all times at a constant rate, would take 30 minutes to travel straight from Ajax to Canton, 35 minutes to travel from Ajax to Canton via Beverly, and 40 minutes to travel from Ajax to Canton via Dilltown. What is the constant rate of the car, to the nearest tenth of a mile per hour.

Please explain how to get this answer VERY well:~)

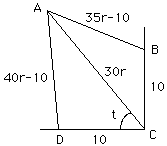
Somehow you have to use the fact that the angle DCB is a right angle and one technique is to use the law of cosines. Let r be the constant rate of the car in miles per minute then the distances are given in the diagram. Using the law of cosines on triangle ADC you get (40r-10)^2 = (30r)^2 + 10^2 - 600r cos t and from triangle ACB (35r-10)^2 = (30r)^2 + 10^2 - 600r cos(pi/2 -t). These equations reduce to 28r - 32 = -24 cos t and 13r - 28 = 24 sin t.

Thus, using the fact that "sine^2 + cosine^2 = 1",
(28r - 32)^2 + (13r - 28)^2 = 24^2.

This is a quadratic in r, which on simplification reduces to
953 r^2 - 2520 r + 1232 = 0. Using the general quadratic you get
r = 0.647384 miles per minute or r = 1.9969 miles per minute, that is
r = 38.8 miles per hour or 119.8 miles per hour.

Cheers
Chris and Harley