Name: Billy
Who is asking: Student
Level: All

Question:
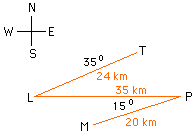
Tom is gold prospector. On his last trip out from town, he headed 35 degree South of West to a lake where he had lunch. The lake was 24 km out of Town. He then headed due East for 35 km before Doubling back on bearing of 15 degree South of west for 20 km to reach his mine. By converting to Cartesian coordinate before doing vector additions do the following:

a) Calculate the position of the mine from town in term of a distance and a direction.
B) How far is the mine from the lake.
C) In which direction would he have to have traveled if he wanted to go straight from the mine?

I drew a diagram with the town labeled T, the lake L, the mine M and the point where he doubles back P. If the origin is at T with the positive y-axis pointing north then the coordinates of L are (24 cos(215 deg), 24 sin(215 deg)) = (-19.66,-13.77). Since P is 35 km east of L, P has coordinates (35 + 24 cos(215 deg), 24 sin(215 deg)) = (15.34,-13.77). Since the mine is 20 km from P in the direction 15 degree south of west, M has coordinates P + (20 cos(195 deg), 20 sin(195 deg)) = (-3.98, -18,94). Now that you have the coordinates of the points T, L, P and M I think that you can answer the questions asked. Cheers Harley