Date: Sun, 27 Oct 1996 12:31:59 -0600 (CST)

Subject: Trigonometry
 
Name:          Lynda 

Who is asking: Parent
Level:         All

Question:
What is the process for solving the following question? As viewed from earth, the sun subtends an angle of approx 32'. If the sun is 93,000,000 miles from earth, find the diameter of the sun.

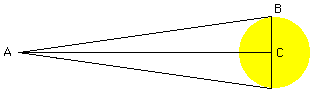
I think there are two ways to approach this problem using your values of 32' and 93,000,000 miles. In the diagram below the angle CAB is 16' and the side AC is 93,000,000 miles so tan 16' is the length BC divided by 93,000,000. Thus BC = 93,000,000 * tan 16' = 93,000,000 * 0.00465 = 432,450 miles and hence the diameter of the sun is approximately 2*432,850 = 864,900 miles.

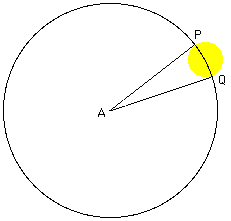
Another approach is to consider the second diagram. Here the angle QAP is 32' or 32/60=0.533 degrees. Thus the ratio of the angle QAP to the angle that takes you once around the circle is 0.533 to 360. Thus the ratio of the length of the arc PQ to the circumference of the circle is also 0.533 to 360.
This gives (arc PQ)/(2*pi*93,000,000)=0.533/360, or
arc PQ = 2*pi*93,000,000*0.533/360 = 865,140 miles.

In either case I get that the diameter of the sun is approximately 865,000 miles.

Cheers,
Penny