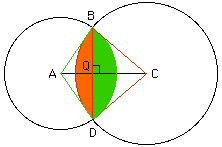
The area of the sector BDC can be found from (area of the sector BDC)/(area of the circle) = (angle C)/(360 degrees). Since the triangle BDC is equalateral, the angle at C is 60 degrees so the area of the sector BDC is (60/360)*pi*(10^2).
Date: Fri, 1 Nov 1996 15:14:12 -0600 (CST) Name: Lynda Who is asking: Student Level: Secondary
Question:
How do I find the area common to two intersecting circles of radii 8 ft and 10 ft
if their common chord is 10 ft long?
If you look at the larger circle in the diagram you can find the area I have shaded orange as the difference between the area of of the sector BDC and the area of the triangle BDC.
 |
Using the fact that BQC is a right triangle find the length of QC and then
the area of the triangle BDC as (1/2)*10 * (the lenght of QC).
The area of the sector BDC can be found from (area of the sector BDC)/(area of the circle) = (angle C)/(360 degrees). Since the triangle BDC is equalateral, the angle at C is 60 degrees so the area of the sector BDC is (60/360)*pi*(10^2). |
Cheers
Penny
To return to the previous page use your browser's back button.