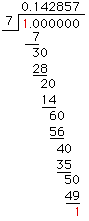
Name: Grant

Who is asking: Teacher
Level: All

Question:
A section about rational and irrational numbers in our algebra II textbook has the folllowing question:

A student who used long division to find the repeating decimal for 1/17 claimed that there were 20 digits in the repeating block of digits. Explain why this is incorrect.

The text book answer is that there can be no more than 16 digits.

The block of repeating digits for 1/17 follows: .0588235294117647

I do not understand why the book would say there can be no more that 16 digits. (I know there are unit fractions with more than 16 repeating digits.) Is this poor wording on the part of the book? Or is there actually a way to tell that the repeating decimal for 1/17 has no more than 16 repeating digits?

Thanks!

The text means that there could be no more than 16 digits when dividing by 17. Similarly they would say at most 72 digits if you were dividing by 73, and so on. Why is this? For simplicity's sake let me use 7 rather than 17 and convince you that the repeating part must have at most 6 digits. When you do the actual long division of 7 into 1, at each stage there will be a (non zero) remainder, and we then 'bring down' a 0 and keep dividing. As soon as one of these remainders repeats, i.e. is the same as an earlier remainder, the decimal expansion will repeat as we are doing the same division we did earlier.

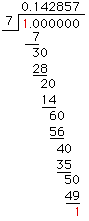
So why at most 6 digits in the repeating part? Because there are at most 6 distinct remainders that can appear ({1,2,3,4,5,6}), implying that by the 7th division we must have a remainder repeated.

Look at 1/2, 1/3, 1/4, 1/5, 1/6, etc. to see that it can be shorter than the number by which you are dividing.

Cheers
Penny