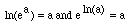Subject: natural logarithm functions

The following two questions are some of my son's homework that he is having trouble with......any advice or assistance would be appreciated.

(eX)5=1000.............the X and 5 are exponents

lnx + ln(x+3) = ln10

There are some basic facts that you have to know about logs and exponentials to solve these problems. First the natural logarithm and exponential functions are inverses, that is

.

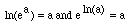Also there are three properties of logarithms that are very useful,

ln(ab) = ln(a) + ln(b), ln(a/b) = ln(a) - ln(b) and

.

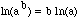For your first problem that 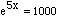take the natural logarithm of both sides to get

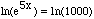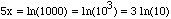, and hence 5x = ln(1000). Using the properties of logarithms this can be written in a simpler form as so x=(3/5) ln(10).

For your son's second problem use the properties of logarithms with

ln(x) + ln(x + 3) = (10) to get ln(x(x + 3))= ln(10).

Now take the exponential of both sides and use the fact that the exponential and natural logarithm functions are inverses to arrive at x(x + 3) = 10. This expression can now be expanded to yield a quadratic equation in x that has two solutions.

You need now to take these values of x and verify that they are solutions to the original problem. The reason that this is important here is that ln(x) is only defined for positive x.

Harley