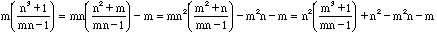 . Therefore if one of
. Therefore if one of 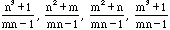 is an integer they all are.
is an integer they all are.
Hello ,
I am Ronald.
Question:
Determine all ordered pairs (m,n) of positive integers such that
( n^3+1)/(mn-1)is an integer.
Thank you very much!!!!!!!!
From ,
Ronald
First note that gcd(n,mn-1) = gcd(m,mn-1) = 1 and
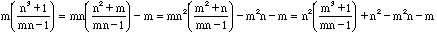 . Therefore if one of
. Therefore if one of 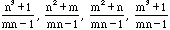 is an integer they all are.
is an integer they all are.
Now suppose that (*)
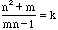 is an integer. Notice that
is an integer. Notice that 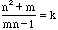 if and
only if
if and
only if
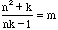 ,
so we can interchange m and k if necessary to get 0<m<=k. Since
,
so we can interchange m and k if necessary to get 0<m<=k. Since
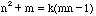 we have
we have
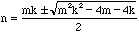 and so
and so
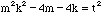 for some integer t >= 0. Thus
for some integer t >= 0. Thus
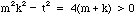 which implies that mk > t and that mk and t are both even or both odd.
Therefore mk - t >= 2.
which implies that mk > t and that mk and t are both even or both odd.
Therefore mk - t >= 2.
Now 2(mk + t) <= (mk-t)(mk+t) <= 4(m + k) <= 8k which implies mk <= 4k and thus m=1, 2, 3 or 4.
For these choices of m the expression 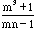 has values
has values 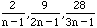 and
and 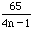 respectively. For these to be integers we have n=2 or 3 in the first case,
1,2, or 5 in the second case, 1 or 5 in the third case and the fourth case in never an integer. Thus from expression (*) the admissible
values of m, n and k are
respectively. For these to be integers we have n=2 or 3 in the first case,
1,2, or 5 in the second case, 1 or 5 in the third case and the fourth case in never an integer. Thus from expression (*) the admissible
values of m, n and k are
| m | 1 | 1 | 2 | 2 | 2 | 3 | 3 | n | 2 | 3 | 1 | 2 | 5 | 1 | 5 | k | 5 | 5 | 3 | 2 | 3 | 2 | 2 |
Richard
To return to the previous page use your browser's back button.