Name: Greg

Who is asking: Student
Level: Secondary

Question:
Which US president developed a proof for the Pythagorean Theorem?

Where can a copy of the proof be located?

The president who constructed a proof of the Pyrhagorean theorem is Garfield. We found the proof in "Elisha Scott Loomis, The Pythagorean Proposition, The National Council of Teachers of Mathematics, 1968". This is a wonderful book. It was first published in 1927, and the 1968 edition published by NCTM is a reissue of the second edition that was published in 1940. The book contains 367 proofs of the Pythagorean theorem. One of these, proof number 231, is attributed to President Garfield. (Loomis has a number of historical notes to justify his claim that this proof is due to Garfield.) What follows is Garfield's proof according to Loomis.

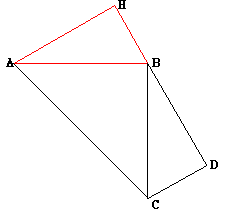In the figure the right triangle is HAB with the right angle at H. Extend HB to D making BD = AH, through D draw DC parallel to AH and equal to BH, and draw CB and CA. The area of the trapezoid CDHA = area of ACB + 2 area of ABH. Therefore (1/2)*(AH + CD)*HD = (1/2)*AB2 + 2*(1/2)*AH*HB or (AH + HB)2 = AB2 + 2*AH*HB, whence AB2 = BH2 + AH2.