Subject: Square Root

Name: Ed

Question:
Every year students ask me 2 questions that I can not easily answer. Can you help?

1. In most texts the solution to a question such as square root x = -6 is

x is undefined.

Yet when teaching to solve
xsquared = 36
x = +6 or -6

There appears to be a contradiction here. My question is when, where and why do we use the principle square root, not both + and -? This often occurs as the extraneous root in the solution of radical equations and in stating the domain and range of functions involving square roots.

2. Are there any simple rules for determining whether equations are functions without graphing them and doing a vertical line test?


Hi Ed

Your first question is one that causes a lot of confusion. The point to remember is that to make 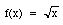a function we define 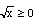regardless of the value of x. The confusion arises, as you said, when solving radical equations which we often do by squaring both sides to arrive at a new equation. With the standard operations that we use in solving equations, adding or subtracting the same quantity from both sides or multiplying or dividing both sides of the equation by a nonstop quantity, the equation produced is equivalent to the original. When we square both sides, the new equation is not necessarily equivalent to the original. The relationship between them is that any solution to the old equation is also a solution to the new, but not vise versa.

The short answer to your second question is no but in some situations it may be easier to approach the problem algebraically rather than geometrically as you suggest. For example the presence of 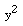in the expression 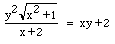makes me think that y is probably not a function of x. Substitution of x=0 gives 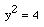so x=2 or x=-2 and my assertion that y is not a function of x is verified.

Harley