Okay, I am in pre-algerbra and I am having a few problems. I was wondering if you could give me some answers and equations. Here are the problems: A circle with a radius of 10m is drawn. A chord is drawn across the circle. How is the area that is formed between the chord and the arc calculated? What is the formula for figuring the area of a circle in terms of circumference?

My name is Staci.

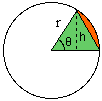If theta is the angle indicated in the diagram expressed in radians then the ratio of the area S of the sector to the area inside the circle is the same as the ratio of the angle theta to 2 Pi, that is S/(Pi r2) = theta/(2 Pi). Hence S=(1/2) (r2) theta. Also if h is the height of the triangle shaded green in the diagram then h/r=sin(theta) so h = r sin(theta) and the area of the triangle is given by (1/2) (r2) sin(theta). Thus the area between the chord and the arc is (1/2) (r2) (theta-sin(theta)).

To find the area of a circle in terms of the circumference use the facts that the area is given by A=Pi r² and the circumference by C=2 Pi r. Now solve the second equation for r and substitute in the first to get the area in terms of the circumference.

Harley

Go to Math Central