Name: Simon
Who is asking: Student
Level: Secondary

Question: Quadratic Graphs

How does varying the values a,b and c affect the graph of
y=ax^2 + bx + c?

It is best to consider the three coefficients, a, b and c separately. I will look at c first, then a and finally b.

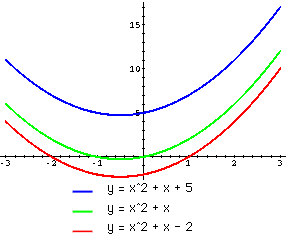
c:	To the right are graphs of y=x^2+x+c for c=-2, 0 and 5. Here it is easy to see that increasing c simply increases y and thus moves the graph vertically upwards.
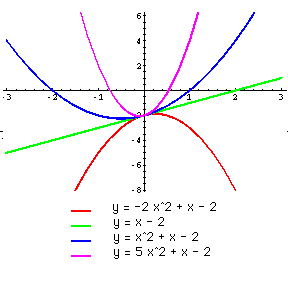
a:	To the right are graphs of y=ax^2+x-2 for a=-2, 0, 1 and 5. The sign of a determines if the parabola opens upwards (a positive) or downwards (a negative). Also you can see that for positive a, as a increases the sides of the parabola become steeper. A similar fact is true for negative a.
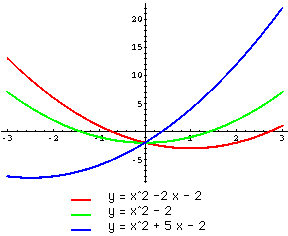
b:	Changing the value of b changes the axis of symmetry of the graph. To the right are graphs of y=x^2+bx-2 for a=-2, 0 and 5. As you can see from the graphs, as b increases the axis of symmetry moves. In fact the axis of symmetry for y=ax^2+bx+c is x=-b/a and thus for the example plotted where a is positive (a=1), increasing the value of b moves the axis of symmetry to the left.

I hope this helps.

Cheers,
Harley