Is there a formula for the area of an equilateral triangle knowing the length of the sides?

Hi Jody,

Euclid tells us that for ANY triangle (and not just an equilateral triangle), once one knows SAS, ASA, or SSS, then one knows everything there is to know about the triangle. Any student who understands these results from Euclid, the Pythagorean theorem and has a pair of scissors can determine her own formula for the area of a triangle.

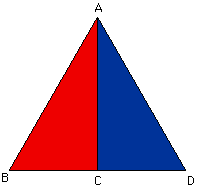
For this particular question where the triangle ABD is equilateral, let AC bisect the angle DAB. Then the triangles ABC and ACD are congruent (SAS). Thus, angles BCA and ACD are equal and have a sum of 180 degrees, so each is a right angle. Now use your scissors to cut along the side AC and flip the triangle ABC over to form the rectangle ACDB.

Thus the area of the triangle ABD is the same as the area of the rectangle ACDB which is its length times its height. Let s is the length of each side of the triangle ABD then |CD|=s/2. The other side of the rectangle, |AC| can be found by using the Pythagorean theorem on the triangle ACD. |AC|^2 + |CD|^2 = |DA|^2, thus |AC|^2 = s^2 - (s/2)^2 = (3/4)*(s^2). Hence the area of triangle ABD is (s/2)*(s*SQRT(3)/2)

Cheers,
Chris and Harley.