Question:
During our math class last week we came accross an equation that we could not graph we were wondering if you could help us try and graph it. The question is:

y=(-2)^x

To deal with the function y=(-2)^x you need to decide what values of x give a real number. Certainly if x is an integer then (-2)^x is real. Also if x=1/3 or x=1/5 then (-2)^x is real but if x=1/2 then (-2)^x is not real. In fact (-2)^x is real if and only if x can be written as p/q where p and q are integers with no common factors other than 1 and q is odd. If x=p/q is such a rational number then (-2)^x=2^x if p is even and (-2)^x=-(2^x) if p is odd.

To see the graph of y=(-2)^x first consider the graphs of y=2^x and y=-(2^x).

The graph of y=(-2)^x is then

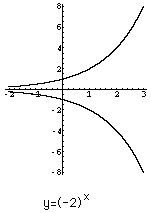
What you don't see in the picture is that the graph has a large number of "holes". The only points on the graph have first coordinate x=p/q where p and q are integers with no common factors other than 1 and q is odd. If p is even the point with first coordinate x=p/q is on the "upper" curve and is p is odd the point with first coordinate x=p/q is on the "lower" curve.

Cheers,
Harley