Sender: Jim
Subject: Multiplying imaginary numbers.
Here is the question:
(square root -2) x (square root -8)
My algebra suggests two possibilities
- combine the roots under one radical getting
= (square root -2 x -8) = (square root +16) = 4
- or rewrite each root using i
= (square root 2 i^2) x (square root 8 i^2)
= i (square root 2) x i (square root 8)
= i^2 (square root 16)
= -1 x 4 = -4
Jim
Teacher, Ernie Studer School
Math 30B
The "square root" notation has a subtle definition that is often misunderstood. The symbol 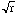 stands for the one and only NON-NEGATIVE number whose square is r. The symbol makes sense only when r satisfies
stands for the one and only NON-NEGATIVE number whose square is r. The symbol makes sense only when r satisfies 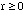 . (There are other situations where restrictions are automatically built in to the notation, for example a/b means that b is nonzero because a/0 makes no sense.)
. (There are other situations where restrictions are automatically built in to the notation, for example a/b means that b is nonzero because a/0 makes no sense.)
Of course, every positive number r has two square roots, namely 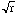 and
and 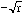 . (For example, to solve
. (For example, to solve 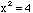 one needs to find both roots, namely
one needs to find both roots, namely 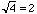 and
and 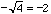 .)
.)
Difficulties arise when it comes to solving the general quadratic equation. For example, the solutions to 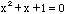 are generally written
are generally written
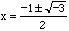 .
.
In order to make sense of a square root of a negative number we INVENT the rule that when r is positive,
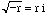 ,
where i is one of two numbers satisfying
,
where i is one of two numbers satisfying 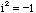 . The other one is denoted by -i, but really these guys are identical twins whom nobody can tell apart. Once you allow negative numbers to have square roots, the symbol
. The other one is denoted by -i, but really these guys are identical twins whom nobody can tell apart. Once you allow negative numbers to have square roots, the symbol 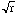 should be avoided, particularly in computations: you lose the important rule that
should be avoided, particularly in computations: you lose the important rule that 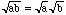 .
.
The difficulty with your problem is what is meant by (square root -2). If you mean any complex number u that satisfies 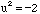 then there are two choices,
then there are two choices, 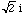 and
and
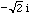 . Likewise there are two solutions to
. Likewise there are two solutions to 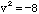 ,
, 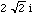 and
and 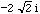 .
.
Thus (square root -2) x (square root -8) could be any of:
- (
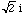 ) x (
) x (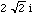 ) = -4
) = -4 - (
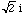 ) x (
) x (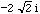 ) = 4
) = 4 - (
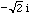 ) x (
) x (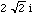 ) = 4 or
) = 4 or - (
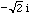 ) x (
) x (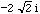 ) = -4
) = -4
Walter, Chris and Harley
To return to the previous page use your browser's back button.