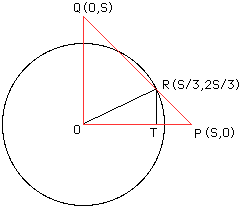
The triangle OPQ has base and height each of length S so its area is (s^2)/2=(900/5)/2=90.
Name: Rebecca
Who is asking: Student
Question:
A circle is centered at the vertex of the right angle of an isosceles triangle. The cirlce passes through both trisection points of the hypotenuse of the triangle. If the length of a radius of the circle is 10, find the area of the triangle.
We have two solotions to this problem.
1. A solution that uses coordinates.

|
Place the triangle OPQ in the plane with the right angle vertex at the origin O, and the two equal sides along the positive axes as in the diagram. Suppose that these two equal sides have length S. Let R be the trisection point of the side PQ closest to P then R has coordinates (S/3,2S/3). Draw a line from R, perpendicular to OP and intersecting OP at T. Then, since OTR is a right angled triangle with hypotenuse of length 10, Pythagoras' theorem gives us 100=(s/3)^2 + (2s/3)^2 or s^2=900/5. The triangle OPQ has base and height each of length S so its area is (s^2)/2=(900/5)/2=90. |
2. A solution without coordinates.
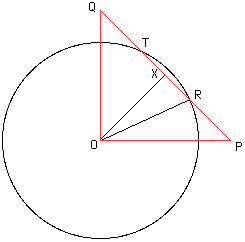 |
Label the triangle OPQ with the right angle at O and let the length of OP be S. Let R and T be the trisection points of PQ as in the diagram and let X be the midpoint of RT. Using the theorem of Pythagoras, the length of PQ is sqrt(2)*S and thus the length of RX is (sqrt(2)/6)*S. Since triangles OPX and OXQ are congruent, angles PXO and OXQ are equal and hence both are right angles. The theorem of Pythagoras for the triangle ORX implies that the length of OX is sqrt(100-(2/36)*S^2). Thus with PQ its base and OX its height the area of triangle OPQ is ((sqrt(2)*2)/2)*sqrt(100-(2/36)*S^2). But with OP its base and OQ its height the area of this triangle is (S^2)/2. Setting these two expressions equal gives s^2=180 and hence the area of triangle OPQ is 90 square units. |
To return to the previous page use your browser's back button.