Name: Erik
Who is asking: Student
Level: Secondary

My typewriter frequently makes mistakes. Suppose I gave you the following system of equations to solve:

35.26X + 14.95Y = 28.35
187.3X + 79.43Y = 83.29

When I looked back, I realized that I meant to use 14.96 as the "Y" coefficient in the first equation instead of 14.95. Solving the system using 14.95 and then solving another system using 14.96 with all other values the same both times results in the intersection points (1776, -4186) and (-770, 1816) respectively.
How can that be?

Hi Erik,

This is a nice problem. It shows how a simple numeric error or round off error can lead to a greatly changed answer. If your missile guidance system finds coordinates by solving equations then an error like this can not only cause the target to be missed, but may send your missile to Tel Aviv rather than Baghdad.

I want to label the three equations

Line 1:	35.26X + 14.95Y = 28.35
Line 2:	35.26X + 14.96Y = 28.35
Line 3:	187.3X + 79.43Y = 83.29

Solving each equation for Y gives,

Line 1:	Y = -2.3585X + 1.8963
Line 2:	Y = -2.3570X + 1.8951
Line 3:	Y = -2.3581X + 1.0486

In this form it is easy to see that the lines are very close to being parallel. Line 3 has slope -2.3581, Line1 is slightly steeper with slope -2.3585 and Line 2 is a little less steep with slope -2.3570.

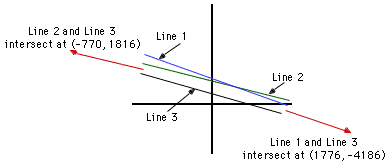
An attempt to plot their graphs shows why the point of intersection of Line 1 and Line 3 is so far from the point of intersection of Line 2 and Line 3.

I have treated the coefficients in the equations as exact, but in most situations the coefficients come from measurements, and reported calculations should not use more significant figures than the original measurements. If this were the case with your example then each line has a calculated slope of -2.36 and hence any intersection point may be artifact of round off error.

Cheers,
Penny