1. What real number exceeds its square by the greatest possible amount?

2. The sum of two numbers is k. show that the sum of their squares is at least 1/2 k^2.

3. The sum of two numbers is k. Show that the sum of one number and the square of the other is at least k- 1/4

4. The vertex of a cone and the circular edge of its base lie on a sphere of radius 5 m. Find the dimensions of the cone of maximum volume that can be fitted into the sphere.

5. Find the cone of largest volume that can be inscribed in a sphere of volume V.

thank you
roger h

roger
oac student in Ontario
I AM A STUDENT. I CAN'T ASK MY TEACHERS BECAUSE THEY ARE ON STRIKE FOR "STUDENTS" other then ME.

Here are a few hints.

1. What real number exceeds its square by the greatest possible amount?

   If the number is x then x exceeds its square by x-x^2, so you need to maximize x-x^2.

2. The sum of two numbers is k. show that the sum of their squares is at least 1/2 k^2.

   If the numbers are x and y then x+y=k so y=k-x. x^2+y^2=x^2+(k-x)^2 is the sum of their squares. Find the minimum of the this function and show it is 1/2 k^2.

3. The sum of two numbers is k. Show that the sum of one number and the square of the other is at least k- 1/4

4. The vertex of a cone and the circular edge of its base lie on a sphere of radius 5 m. Find the dimensions of the cone of maximum volume that can be fitted into the sphere.

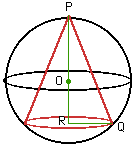   	Let the center of the sphere be O, the height of the cone be h and the radius of its base be r. Consider the triangle PRQ.
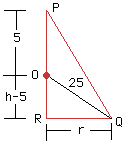   	Using the theorem of Pythagoras on triangle ORQ you get that (h-5)^2 + r^2 = 25, or r^2 = 25 - (h-5)^2. Since the volume of the cone is V=1/3 Pi r^2 h you can use the expression for r^2 to write V as a function of h alone.

5. Find the cone of largest volume that can be inscribed in a sphere of volume V.