Date: Sun, 11 Jan 1998 11:25:32 -0600 (CST)
Name: james
Who is asking: Student
Level: Secondary
Question:
A hexagon inscribed in a circle has three consecutive sides each of length 3 and three consecutive sides each of length 5. The chord of the circle that divides the hexagon into two trapezoids, one with three sides each of length 3 and the other with three sides each of length 5, has length equal to m/n, where m and n are relatively prime positive integers. Find m+n.
(a) 309 (b) 349 (c) 369 (d) 389 (e) 409
Hi James,
In Figure 1 X is the center of the circle. Let C = m/n be the length of PS. Since the chord TU subtends the angle theta at the center and the angle UPT at the circumference, angle UPT = theta/2. Since |TS|=|UT|=3, angle TPS is also theta/2. Hence angle UPS = theta.
By a simular argument angle SPQ = phi. |
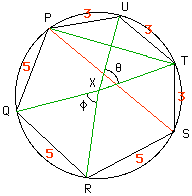
Figure 1
|
In Figure 2 R is the radius of the circle. Thus, since angle YXU = theta/2, |YU|/|UX|=sin(theta/2) and thus 3 = 2 R sin(theta/2). Simularly using triangle XQR 5 = 2 R sin(phi/2). Thus
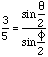 - - - Equation 1. - - - Equation 1.
|
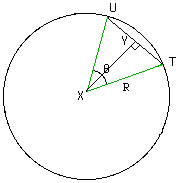
Figure 2
|
In Figure 3 |PA|/|UP|=cos(theta) and thus |PA|=3 cos(theta). Simularly |BS|=3 cos(theta) and hence C=|PS|=3+6cos(theta). Using the fact that
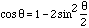 we get 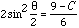 - - - Equation 2. - - - Equation 2.
Simularly 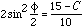 - - - Equation 3. - - - Equation 3.
|
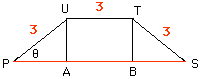
Figure 3
|
Thus, using equations 1, 2 and 3 we get
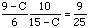
or m/n = C = 360/49 and hence m+n = 409.
Cheers,
Haragauri
Go to Math Central
To return to the previous page use your browser's back button.


![]() - - - Equation 2.
- - - Equation 2.![]() - - - Equation 3.
- - - Equation 3.
