

From Jessica
Grade 11 student
There's a question I have that I hope you can answer about calculating area.
It seems to me that common sense says that if you have say 100 meters of fence, the area you can enclose should be a constant. Yet the math says it is not so. For example if you build a rectangle 10x40 the enclosed area is 400 square meters. But if you build a rectangle 5x45 then the area is 225 square meters, even though you've started with the same amount of fencing.
I know this is true, but can anyone explain IN ENGLISH why this is so?
thank you
Hi Jessica
Let me try it with some pictures.
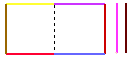
| Suppose that you have you have 8 meters of fencing. You can use it to enclose an area of 2 square meters as in the diagram. |  |
|
| You can now push the 2 squares together and remove the center 2 sections of fence to maintain an enclosed area of 2 square meters but with two section of fence unused. |  |
|
| Now push the bottom two sections of fencing down and insert the unused 2 sections. This gives you have an area of 4 square meters enclosed by the 8 meters of fencing. |  |
|
| Here's another example. | ||
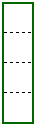
| Suppose that you have 10 meters of fencing, some squares that are 1 meter by 1 meter and you want to surround as many of the squares as you can using the fencing. You can use the fence to surround 4 squares (4 square meters) as in the diagram. Notice here that 2 of the squares have a section of fence on 2 sides each and the other two squares have fence on 3 sides each. |  |
|
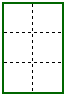
| The configuration on the right makes more efficient use of the fencing and surrounds an area of 6 square meters. Here 2 of the squares have a fence on only 1 side only, and the remaining 4 have fencing on 2 sides. By packing the squares closely together rather than stringing them out in a line more efficient use is made of the fencing and thus a larger area is surrounded. |  |
|
To return to the previous page use your browser's back button.