1. A and B are matrices. If A^n=B^n, can we say A=B or det(A)=det(B) or det(A)^n=det(B)^n ? Any conditions ???

2. If B^(-1) is the inverse of B, where B is a matrices. Can we say [(B^(-1))^n][B^n]=I, where I is identity matrices? Any conditions???

Hi,

For your first question it is instructive to first consider the problem for real numbers A and B. For example, if A=1 and B=-1, then A^2=B^2 yet A and B are not equal. This situation is even worse with complex numbers: let A=1 and B= , where i^2 = -1. In this case A^3=B^3, yet neither A equals B nor A^2 equals B^2.

We can extend these ideas to matrices. Let

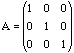and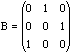

Then, again, A^3=B^3. Observe that not only is B different from A, but B is not even a scalar multiple of A; that is, A and B are linearly independent.

Now what about determinants? If A^n = B^n, then det(A^n)=det(B^n), which, by using the fact that the determinant of a product is a product of determinants, says that (det A)^n= (det B)^n. Thus with matrices of real numbers, det(A) is either det(B) or -det(B); with matrices of complex numbers, det(A) is z det(B), where z is a complex number of modulus 1.

To see what to do with the second question try it with n=2. Here

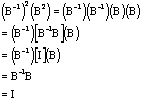
Now it should be clear what to do for any positive integer n.

Cheers,
Doug