How do you find the area of a pyramid?

Student asking
grade 10
My name is Lisa

Hi Lisa

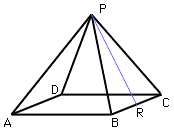
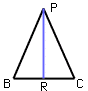
	To find the surface area of a pyramid with a square base as in the diagram you need to add the area of the base and the areas of the four triangular faces. If |AB| = |BC| = |CD| = |DA| = a then the area of the base is a2 square units. If you know the "slant height" |BP| = s of the pyramid then to find the area of the face PBC you need its height h = |PR|.
	Since PBR is a right triangle the theorem of Pythagoras tells us that s2 = h2 + (a/2)2. Thus if you know a and s you can find h = Sqrt(s2-(a/2)2) and the area of PBR which is 1/2 bxh. Thus the surface area of the pyramid is a2+4(1/2 bxh).

Cheers,
Harley