Name: Shameq

Who is asking: Student
Level: Secondary

Question:
Hi,

I've got a couple of problems which I hope you'll be able to solve for me.

I'm investigating pythagorean triples, and I have found a trend for the triples themselves, and thus have been able to form a general equation, i.e. a=2x+1, b=2x^2+2x, and c=b+1. Now, I sure this equation works, because I've tried it out and have come up with triples that adhere to a^2 + b^2 = c^2. But I was wondering WHY c=b+1. Is it possible to have c=b+2, and if not why not? THAT is the first problem.

My second problem: Is there a general equation to express the relationship between a triple and its perimeter, i.e.
(3, 4, 5), P=12
(5, 12, 13), P=30
(7, 24, 25), P=56
(9, 40, 41), P=90
etc.

If there is an equation is there also a proof for it?

Also is there a general equation to express the re;ationship between a triple and its area, i.e.
(3, 4, 5), A=6
(5, 12, 13), A=30
(7, 24, 25), A=84
(9, 40, 41), A=180
etc.

If there is an equation for this, is there a proof as well?

Thanks loads,

We first find all "primitive" Pythagorean triples: these are triples of numbers a, b, c with no common divisor except 1 that satisfy . Note that for primitive triples one of a and b must be even, the other odd. For each pair of integers r,s with

(a) 0 < r < s
(b) not both odd and
(c) having no common divisor greater than 1,
(This latter condition we write (r,s)=1.)

then is a primitive Pythagorean triple. Moreover, all primitive Pythagorean triples look like this when a is even. It follows that the complete set is

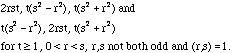
You found the subfamily with s=a+1, and r=a. You can play around with these equations and get , so yes, c=b+1 is possible.

For primitive triples perimeter = and area = .

A good reference for this material is the American Mathematical Monthly, Volume 94, Number 9, November 87, 869-871.

Cheers,
Chris.