I'm a math teacher in Jerusalem, Israel.

I'm teaching about graphing polynomial functions in a pre-calc class. A student asked me what they're good for. I couldn't give her a good example. Do you have one. Thanks.

Polynomials form an extremely important class of functions. They are used themselves in many applications and as building blocks in other applications. Here are a few examples.

A parabola is the graph of a quadratic polynomial, y = a x^2 + b x + c and there is a note in the Resource Room called Why are satellite dishes parabolic? that explains why this shape is so important.

Another application of quadratic polynomials is in Newtonian motion. For example if you are on a cliff and throw a ball upwards then Newton's Laws tell us that the height of the ball (in meters) t seconds later is given by the quadratic polynomial
h(t) = 4.9 t^2 + u t + s
where u is the velocity with which you threw the ball in meters per second, and s is the height of the cliff in meters. We are assuming in this example that air friction can be ignored.

In many situations a scientist, Engineer, or economist might have some data points and want to draw a curve through them or better yet find a mathematical expression for a curve that passes through the points.

If you just need to sketch a curve then you start at one end and either freehand or with some "curved ruler" you draw a smoothe curve, that is a curve without sharp corners, that passes through the points..

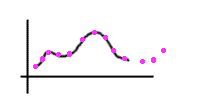
To find a mathematical expression you can apply a similar technique. Start at one end and draw a piece of a cubic polynomial from the first to the second points. Now draw a piece of a cubic polynomial from the second to the third point making sure that where they come together, at point number two, that they don't make a sharp corner. Now extend this procedure from the third to the fourth point and so on. In this way we get a mathematical expression for a smooth curve through the points that is not a polynomial but it is built from cubic polynomials. This curve is called a cubic spline.

I hope this helps,
Penny.