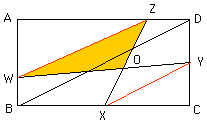
ABCD is a rectangle. X and Y are the midpoints of BC and CD respectively. W is a point on AB such that AW : WB = 2 : 1. Z is a point on AD such that AZ : ZD = 2 : 1.

WY intersects XZ at O. If the area of triangle WOZ is 84 centimeters squared, find the area of triangle XOY.

Please help me. I'm a student (Ong Shimin) who need a solution urgently. This is a secondary question.

E-mail me at ongpcn@mbox4.singnet.com.sg

Thank you,
Shimin

Triangles DBC and YXC are similar and triangles ABD and AWZ are also similar. It follows that XY and WZ are parallel and thus triangles ZWO and OXY are similar. Since XC/AZ = (1/2)/(2/3) = 3/4 the sides of triangle OXY are 3/4 as long as the sides of triangle ZWO. This implies that the area of triangle OXY is (3/4)^2 times the area of triangle ZWO, thus 84*(3/4)^2 = (9*21)/4 = 47.25.

Cheers,
Chris.