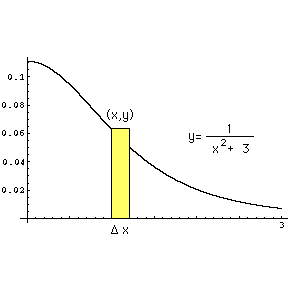
where r is the radius of the disk, which here is the height, y, of the yellow strip.
Since the variable of integration is going to be x I need to express the volume of the disk in terms of x. Thus
Hi, I seem to be stuck again
I'm on the section fpr The Computation of Volumes of Solids of Revolution and the following question is giving me problems:
-Consider the region in the first quadrant bounded by the x-and y-axes, the vertical line x=3, and the curve y=1/(xsquared + 3) I can determine the volume of the solid by rotating the region about the y-axis using the shell method but I can't seem to be able to get started with the volume when rotated about the x-axis.
The same problem arises with the following question: -consider the region in the first quadrant bounded by the x- and y-axis, the curve y=xe(to the -x) and the line x=b. For this one I assumed that I could pick any number for b and it worked fine for the y-axis again using the shell method. But when I try to use the disk method for the x-axis it just does not work or I'm setting it up wrong.
Any insights would be greatly appreciated. Thanks.
Lorraine
Hi Lorraine
|
To find the volume when rotated about the x-axis by the disk method I use the diagram on the right. Rotating the strip shaded yellow about the x-axis gives a disk with volume where r is the radius of the disk, which here is the height, y, of the yellow strip. Since the variable of integration is going to be x I need to express the volume of the disk in terms of x. Thus |
 |
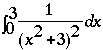 .
.
Cheers
Harley
To return to the previous page use your browser's back button.