Name: Jason

Who is asking: Student
Level: Secondary

Question:
I was looking at the relationship of the area of a circle and the circumference when I realized that 2*pi*r is the derivative of pi*r^2. I was wondering if there is any connective deep dark meaning as to why this appears to be related. Thanks for any help you can give me!

Jason

Hi Jason Yes there is a deep connection related to integration.   Think of the area of the circle composed of a series of very thin rings of standard thickness . At a distance (radius) h from the center, the ring has length and thickness - and is roughly (if you stretch it out like a thin string) of area .   Now add up all these rings (integrate over h) and you have = ! A similar connection holds between the surface area of a sphere and the volume of a sphere.   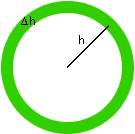You can also do this for a square - provided you set up the origin as the center of the square and x as half the length of a side. The layers are smaller squares of perimeter 8 h at distance h from the center. The area of thin square ring is 8 h and the total area is then - the actual area of a square with sides 2x.   Try it with some other shapes. The key is a consistent breaking up of the object into thin strips of thickness . Integrating the lengths of these strips from the smallest to the largest, with respect to h then gives the area.   This connection is nice for reducing memory work: remember one formula and get the other by differentiation or integration! It also leads on to some important insights and methods of integration as you learn more calculus. Walter