A Tightrope Walker.

Date: Wed, 18 Feb 1998 12:05:48 EST
Subject: ap calculus for high school

I am a parent, Amy. I have a problem which I am trying to assist my child in solving:

A tightrope is stretched 30 feet above the ground between the Jay and the Tee buildings, which are 50 feet apart. A tightrope walker, walking at a constant rate of 2 feet per second from point A to point B, is illuminated by a spotlight 70 feet above point A.
(a) how fast is the shadow of the tightrope walker's feet moving along the ground when she is midway between the buildings? (Indicate units of measure)
(b) how far from point A is the tightrope walker when the shadow of her feet reaches the base of the Tee building? (Indicate units of measure)
(c) how fast is the shadow of the tightrope walker's feet moving up the wall of the Tee building when she is 10 feet from point B? (Indicate units of measure)

Thank you for any help you can offer.

Hi Amy

I drew a diagram of the situation and labeled it. You have W increasing at the rate of 2 feet per second, ie W'=2 feet per second. Triangles DCA and DEF are similar so W/70=X/(70+30). Thus 70X=100W. Differentiating with respect to time gives 70X'=100W'=100(2) and hence X'=20/7 feet per second.
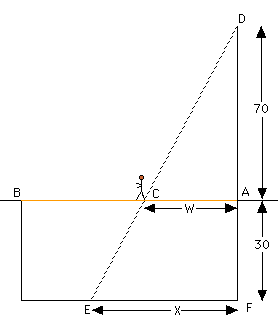
Notice that this result does not depend on the value of X so the shadow is moving along the ground at a constant rate of 20/7 feet per second.
When the tightrope walker is far enough that the point E is on the wall of the building say Y feet up from the ground (you need to redraw the diagram), triangles DCA and CBE are similar. This should allow you to find the rate at which E is moving up the wall.
Cheers
Harley

A tightrope is stretched 30 feet above the ground between the Jay and the Tee buildings, which are 50 feet apart. A tightrope walker, walking at a constant rate of 2 feet per second from point A to point B, is illuminated by a spotlight 70 feet above point A.
(a)	how fast is the shadow of the tightrope walker's feet moving along the ground when she is midway between the buildings? (Indicate units of measure)
(b)	how far from point A is the tightrope walker when the shadow of her feet reaches the base of the Tee building? (Indicate units of measure)
(c)	how fast is the shadow of the tightrope walker's feet moving up the wall of the Tee building when she is 10 feet from point B? (Indicate units of measure)