Hi.
I would like to know what is the square root of i , and i squared? I am looking for a response appropriate for secondary level students.

Thank you,
Wayne

Hi Wayne
The answer to your second question is straightforward since i is, by definition, one of the two numbers satisfying i squared is -1, the other is -i. Thus the answer to your second question is that i squared is -1. The first question requires more work but should be appropriate for secondary level students if they know some trigonometry.

  
  Complex numbers can be written in the form a+ib where a and b are real numbers. This gives rise to a graphical way to represent complex numbers in what is called the complex plane. Draw a coordinate system as you would for the Cartesian plane but label the horizontal axis the real axis and the vertical axis the imaginary axis. The complex number a+ib is then representated in the complex plane by the point with coordinates (a,b).  
  For points on the unit circle (points at a distance 1 from 0) you can use some trigonometry to get a particularly useful representation. For a point z on the unit circle measure the angle (counterclockwise) between the positive real axis and the line segment joining z to 0. This angle, written , is called the argument of z and then . Now what happens when you multiply two such numbers? If

and

then,expanding as you normally would, using the fact that i squared is -1 and using the double angle expressions for sine and cosine, gives

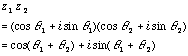
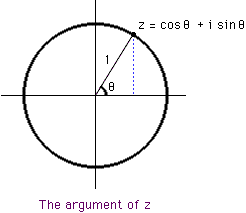
Hence is the complex number on the unit circle with argument 		 
  Now back to your questions.
  • First check, using this method, that i squared is -1. The complex number i has argument 90 degrees and hence i.i has argument 90 + 90 = 180 degrees. Hence i squared = cos(180 deg) + i sin(180 deg) = -1.
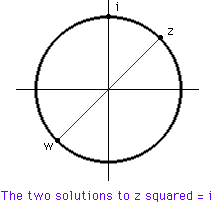
  • For your first question you want z.z=i. Since the modulus of i is 90 degrees taking z with modulus 45 degrees will work, Hence
    z = cos(45 deg) + i sin(45 deg) and thus

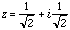
    There is, however, another possible choice for z, and that is with modulus 225 degrees, since doubling this angle also brings you around to i. Thus a second solution to i squared = -1 is then
    w=cos(225 deg) + i sin(225 deg) and thus

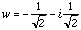
    You can check both solutions by calculating z times z and w times w.

Cheers,
Harley 		 

Go to Math Central

To return to the previous page use your browser's back button.