Who is asking: Other
Level: Secondary

Question:
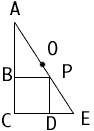
There is a cube box 3feet x 3feet x 3ft resting against a vertical wall on level ground. Resting against the outside corner of the box is a ladder 10 feet tall, this ladder is of course resting on the ground but also against the outside corner of the box and rests on the wall.

The question- the ladder is divided into two unequal section bounded by the box to the ground and the box to the wall. what are those dimensions?

Hi Michael

In the diagram on the right O is the center of the ladder so |OA|=5. Let |PO|=t and |AB|=a. Since triangles ABP and PDE are similar and |DP|=3, Also since triangle ABP is a right angled triangle, the theorem of Pythagoras gives (5+t)2 = a2 + 9. Solving the first equation for a and substituting into the second gives Multiplying both sides by (5-t)2 and simplifying gives the quartic equation t4 - 68 t2 + 175=0 Using the general quadratic to solve for t2 yields and hence Thus |PA| = 5 + t = 3.36, 6.64, -3.08 or 13.08. Hence the point P divides the ladder into two pieces of length 3.36 and 6.64.

Cheers
Penny