Who is asking: Teacher
Level: Middle

Question:
My Grade 8 class and I were discussing the solution to the following problem:

What is the area of the largest equilateral triangle that can be drawn on a 5 cm square.

We used 5 cm as the base of our triangle and then drew the other two legs of 5 cm each to make the equilateral triangle. We then drew an altitude from the upper vertex to the base of the triangle. Using the law of Pythagoras with side a of 2.5 and side c of 5 we calculated side b to be 4.3 cm (the altitude). Therefore the area of the triangle would be 5 x 4.3 divided by 2 or 10.75 square cm.

The answer key to this resource says I am wrong.

What do you think? Have we interpreted the question incorrectly?

Hi Ed,

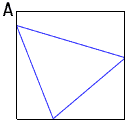
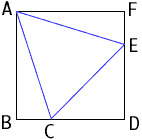
Try to draw the largest equilateral triangle you can on the square with no side parallel to a side of the square. If the picture you draw looks like the diagram on the right then it seems you can make a larger triangle by sliding it up to put the vertex at the vertex A of the square, and then rotating the triangle clockwise to allow it to grow larger. The resulting picture looks like the second diagram. If the triangle is equilateral then |AC| = |EA| and since triangles ABC and EFA are right angled, they must be congruent. Thus angle CAB = angle FAE = 15o. The question then is can you put an equilateral triangle in this position?    Starting with the aquare ABCD Draw the lines AE and AC so that angle CAB = angle FAE = 15o. Hence angle EAC = 60o. Since |FA| = |AB|, angle CAB = angle FAE and triangles ABC and EFA are right angled these triangles are congruent and thus |EA| = |AC|. Hence angle CEA = angle ACE. Since angle EAC = 60o it follows that angle CEA = angle ACE = 60o. Thus triangle ACE is an equilateral triangle. Cheers Chris and Harley