Subject: combinations
Name: Beth
Who is asking: Parent
Question:
We have 6 groups meeting at three different places simultaneously. The meetings take place once a month each year. Is there a way to have each group meet with each of the other groups at least twice in a year, four times in each place?
Hi Beth,
Suppose that the groups are called A, B, C, D, E and F. Imagine them arranged around a wheel with A in the center as in the diagram. The lines indicate that in the first month A will meet with F, B with E and C with D. These three meetings are designated AF, BE and CD.
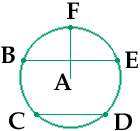
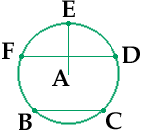
Continue to rotate the groups around the wheel for the third, fourth and fifth months to produce five months of three meetings each. These meetings can be arranged at three places as follows.
| Place | |||
|---|---|---|---|
| Month | I | II | III |
| 1 | AF | BE | CD |
| 2 | DF | AE | CB |
| 3 | AD | CE | BF |
| 4 | EF | BD | AC |
| 5 | CF | AB | DE |
In scheduling the five months of meetings at the three places an attempt has been made to minimize the number of times each group is in any one place.
For the second five month period shift the columns in the schedule above so that the meetings that were scheduled at II in the first five months are sceduled at I in the second five months, the meetings that were scheduled at III in the first five months are sceduled at II in the second five months and the meetings that were scheduled at I in the first five months are sceduled at III in the second five months. For a third five month period shift the columns again as in the diagram. With this schedule each group meets with each other group exactly three times, once in each place and each group is in each place exactly five times.
| Place | |||
|---|---|---|---|
| Month | I | II | III |
| 1 | AF | BE | CD |
| 2 | DF | AE | CB |
| 3 | AD | CE | BF |
| 4 | EF | BD | AC |
| 5 | CF | AB | DE |
| 6 | BE | CD | AF |
| 7 | AE | CB | DF |
| 8 | CE | BF | AD |
| 9 | BD | AC | EF |
| 10 | AB | DE | CF |
| 11 | CD | AF | BE |
| 12 | CB | DF | AE |
| 13 | BF | AD | CE |
| 14 | AC | EF | BD |
| 15 | DE | CF | AB |
Your question asked for twelve months with each group meeting each other group at least twice a year, four times in each place. To do this duplicate the first ten months from the fifteen month schedule above. In this ten month period groups A, E and F are in place I four times, groups B and D are in place I three times and group C is in place I only twice. Thus in the remaining two months meetings BC and CD need to be scheduled at I. Simularly in the remaining two months AF and DF need to be scheduled at II and AE and BE need to be scheduled at III. Thus the following schedule will meet your requirements.
| Place | |||
|---|---|---|---|
| Month | I | II | III |
| 1 | AF | BE | CD |
| 2 | DF | AE | CB |
| 3 | AD | CE | BF |
| 4 | EF | BD | AC |
| 5 | CF | AB | DE |
| 6 | BE | CD | AF |
| 7 | AE | CB | DF |
| 8 | CE | BF | AD |
| 9 | BD | AC | EF |
| 10 | AB | DE | CF |
| 11 | BC | DF | AE |
| 12 | CD | AF | BE |
Cheers
Chris and Harley