To: QandQ@MathCentral.uregina.ca
Hello my name is Kirk from Scarborough, Ontario.
I have been out of a formal education system for thirty years. I program microcontrollers in my spare time. I have built a temperature sensing device ready to go but, thermistors are very non-linear. I do know that there is a way to calculate the input condition of the thermistor and display the correct temperature in degrees C. I am sending a file to show my progression so far.
(T is temperature in degrees C and R is resistance in Kohms.)
| T | R | T | R | T | R | T | R | |||
|---|---|---|---|---|---|---|---|---|---|---|
| -50 | 325.2 | -10 | 42.45 | 30 | 8.313 | 70 | 2.229 | |||
| -45 | 247.5 | -5 | 33.89 | 35 | 6.941 | 75 | 1.924 | |||
| -40 | 188.4 | 0 | 27.28 | 40 | 5.828 | 80 | 1.669 | |||
| -35 | 144.0 | 5 | 22.05 | 45 | 4.912 | 85 | 1.451 | |||
| -30 | 111.3 | 10 | 17.96 | 50 | 4.161 | 90 | 1.366 | |||
| -25 | 86.39 | 15 | 14.68 | 55 | 3.537 | 95 | 1.108 | |||
| -20 | 67.74 | 20 | 12.09 | 60 | 3.021 | 100 | .9735 | |||
| -15 | 53.39 | 25 | 10.00 | 65 | 2.589 | 105 | .8575 | |||
| 110 | .7579 |
Kirk
Hi Kirk
I plotted the temperature (T) and resistance (R) data that you sent and indeed the relationship is non-linear as you indicated.
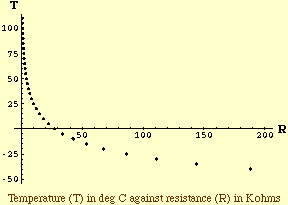
One way to approach this problem is to attempt to linearize it and then use linear regression to fit a line. To do so you need to recognize the functional form from the shape of the plotted data. The plot of your data resembles a log curve so my initial conjecture is that the functional form is T = A + B Log(R) where A and B are constants and Log is the natural log function. (You could just as easily use the common log, that is the log base 10.) I then took the log of each R value and plotted Log(R) against T.
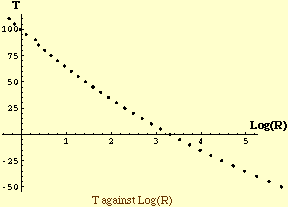
This plot does appear approximately linear and performing a linear fit (linear regressiion) produces T = g(R) = 91.97 - 26.43 Log(R). Plotting this function with the data points shows a reasonable fit but I think we can do better.
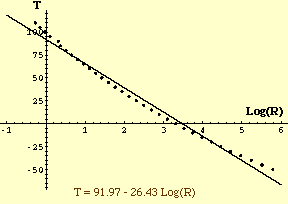
For each data point measure the vertical distance between the point and the line, that is for each data point compute T-g(R). Now plot T-g(R) against Log(R) to get
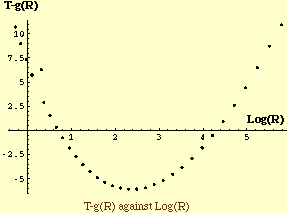
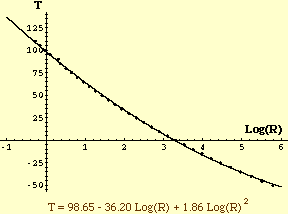
This plot resembles a parabola T - g(R) = C + D Log(R) + E Log(R)^2 and hence, collecting like terms, perhaps a better functional form is T = P + Q Log(R) + R Log(R)^2. This time a two variable linear fit produces T = 98.65 - 36.20 Log(R) + 1.86 Log(R)^2 and its graph indicates a much better fit to the data.
Harley
To return to the previous page use your browser's back button.