Hello my name is Stephen and I have some questions on slopes of curved lines. Any help would be greatly appreciated.

When one plots the graphs of:

1. Can a point on a defined line (graph) have its own slope?

2. What is the slope or degree measure of a point on a defined circle? (189.99... or 180 degrees?.....?)

3. When one plots the graphs of y=2^x, y=3^x, y=x^x When each of these graphs pass through point (0,1) do they have the same slope? I know they are different lines but is it possable that they have the same slope at point (0,1).

4. Can they have a slope at only one point ?

Cheers,
Stephen

Hi Stephen,

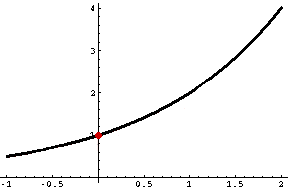
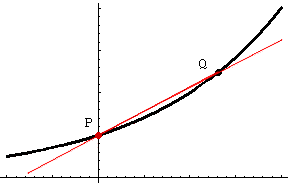
The concept of slope really applies to straight lines. For a curve that is not a straight line "the slope of the curve at a specific point" is the slope of the tangent line at that point. The top diagram at the right is the graph of y = 2x and the slope of this graph at the point (0,1) is the slope of the tangent line at (0,1).    Approximating the slope of the tangent line to the curve at (0,1) is stratghtforward. Let (0,1) be P and let Q be some other point on the curve close to P. Find the slope of the line joining P and Q. If P and Q are very close then the line joining P and Q is very close to the tangent line. For example if Q is the point (0.01,20.01) then the line joining P and Q has slope (20.01 - 1)/0.01 = 0.6956. Try some other values for Q even closer to P and you will see that the slope of the tangent at P is approximately 0.6931.    Now try the same exercise with the graph of y = 3x. This time you should find that the slope of the tangent line at (0,1) is approximately 1.10. I hope this helps, Harley