Name: Angela
Who is asking: Student
Level: Secondary

Question:
The full question is this: Isaac Newton generalized the Binomial Theorem to rational exponents. That is, he derived series of expansions for such expressions as (x+y)^-3 (x+y)^2/3 (x+y)^5/6 What did Newton find? What are the first four terms of the series expansions of binomials above? How can this extended Binomial Thrm. be used to aid in calculations?

First, I expanded the (x+y)^-3 and got:

1/(x³+3xy+3xy²+y³)

But I don't know how to expand the last two. I tried to and got:

(x² + 2xy + y²)/(cubed root(x+y)) ???

I don't know if I did those right. I don't understand how this relates to the Bionomial Thrm. and what Newton found. Please help me! I'm desperate!! Thank you so much!

Hi Angela

For n a positive integer and

the Binomial Theorem states that

Newton generalized this for n not a positive integer. The easiest example comes from looking at the identity

which is valid provided x is not 1. To see that this is valid multiply both sides by 1-x.
   Now what happens as n tends to infinity? If -1<x<1 then, as n tends to infinity, xⁿ tends to zero and it seems reasonable that

(Why can't x = -2 or 3 ?)

This agrees with the pattern in the statement of the binomial theorem above if a = 1, b = -x and n = -1

It was this kind of observation that led Newton to postulate the Binomial Theorem for rational exponents.

For your first example write (x+y)^-3 as x^-3(1+y/x)^-3, expand (1+y/x)^-3 using the Binomial Theorem as above:

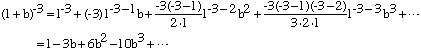
with b = y/x and then multiply each term by x^-3.

Simularly for fractional exponents. For example in your second problem write (x+y)^2/3 as x^2/3(1+y/x)^2/3 and use the Binomial Theorem to expand (1+y/x)^2/3.

You need to know some calculus to study the Binomial Theorem for rational exponents and to determine for what values of x it is true.

I hope this helps,
Penny