Date: Tue, 29 Dec 1998 19:34:24 EST
Subject: pythegorean theorem research project

Hi my name is Mohammed. I am a math honors student in 8th grade. I have to do a research project in math. The only problem is that I have to do the research project at a 10th grade level. I am having trouble raising the project at a tenth grade level. Would you please kindly take your time to give me some tips and web sites that will help me raise the Pythagorean theorem to a 10th grade level. Would you please e-mail me back at Yanks21109.

Thank You for you time,
Mohammed

Hi Mohammed
I have a number of suggestions for you.

Frist from Jack

Try this.

  You know that Pythagoras said that the square drawn on the hypotenuse has an area equal to the sum of the areas of the squares drawn on the other two sides.
  Investigate the semi-circle drawn on the hypotenuse and compare its area to the sum of the areas of the semi-circles drawn on the other two sides. Surprise!
  Now, on each side of the right-angled triange draw a rectangle such that the height is twice the base. Compare the area of the rectangle drawn on the hypotenuse to the sum of the areas of the rectangles on the other two sides. Surprise!
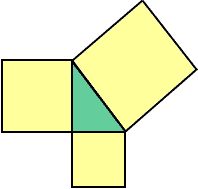
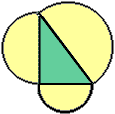
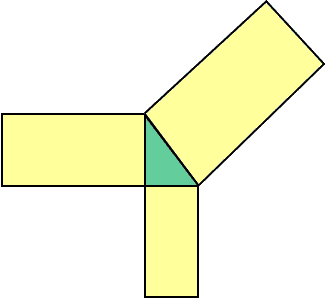
  Repeat for rectangles that have the height:base = 3:1.Repeat for 1:2, etc Now draw an equilateral triangle on each side and repeat. Try it for a hexagon. You may soon see that the secret has to do with the fact that the figures are similar (i.e. have the same shape).
  Have fun!
Jack

Second from Walter

One way to raise the level would be to investigate what happens when the angle is NOT 90 degrees.

  • If the angle is < 90, then a^2 + b^2 > c^2
  • If the angle is > 90, then a^2 + b^2 < c^2.
Euclid's proof, using parallelograms can be adapted to give these inequalities, once you notice how the changes in the angle opposite the hypotenuse result in changes in c. This is nicelyu done in a dynamic geometry program, like geometer's sketchpad. With this extension, you can apply the Pythagorean Theorem to compare the areas of, say two medium pizza's with one large pizza. Place the diamaters of the medium pizza along the two sides around the angle, and the diameter of the large pizza along the hypotenuse.
  • If the resulting angle is 90 - the area's are equal.
  • If less than 90, the two medium are larger.
  • If more than 90, the large is larger!
You need to see why the theorem works for areas of other shapes (like circles, equilateral triangles, etc.)

Here is a second direction. One use of pythagoris is as a CONSTRUCTION of a new square with the area of the sum of the areas of two smaller squares. Some people think that that was the Greek use of the theorem - to constructively add squares. Now look at how to change triangles into squares of the same area (constructively). With that, you can take any polygon, divide it into triangles, change them into squares and add them. The goal is to prove that ANY polygon can be constructively changed into a single square of the same area.

A consequences is that any two polygons of the same area can be cut up and reassembled into the same square (or one another) in a finite number of steps. This is called 'dissection' and 'equidecomposibility' in the geometry texts. In case you think this is obvious - tha analogous statement about objects in 3-space is WRONG!

Walter

And a footnoteote:

If you go to the Quandaries and Queries section of Math Central and search in the keyword field for Pythagoras you will find some questions and answers concerning Pythagoras. Three of them might be of interest.

  • Presidental Proof:
    There is a proof of the Theorem of Pythagoras that comes from an American president. Can you guess which president?
  • Triangles the Pythagorean Theorem and Pizzas
    Dont read this until after you have "investigated the semi-circle drawn on the hypotenuse" as suggested by Jack
  • Euclid's Pythagorean Proof
Cheers
The Centralizer

Go to Math Central

To return to the previous page use your browser's back button.