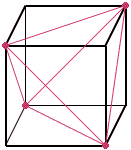
In analyzing a cube, I would like to find a tetrahedron inscribed in the cube which has none of its faces in the planes of the faces of the cube. I would like to see this tetrahedron outlined in the cube.

My name is Jane. I am an elementary education student.

Thank you!

Hi Jane, The cube has eight vertices. Take four of them, which do not share any edge of the cube (e.g. two opposite vertices of the top square and two of the bottom - which are NOT below the chosen top vertices).    Now consider these vertices as vertices of a tetrahedron. You will find that the six edges you are looking for are six diagonals of the six faces, joining the selected vertices.    You will also find that you have 'chopped off' the other four vertices with a plane through its three neighboring vertices, leaving behind the four cuts as the four faces of the tetrahedron.

Walter