Date: Wed, 20 Jan 1999 15:46:25 -0600 (CST)
To: QandQ@MathCentral.uregina.ca

Name: jen

Who is asking: Student
Level: Secondary

Question:

  • How do u find the interior angles of a pentagon when you are given 4 of the angles and you need to find the fifth?

  • If you are given the measure of each exterior angle of a regular polygon, how do you figure out how many sides the polygon has?

  • i need all information on polygons and how to find their angles!!!
Thankyou for all ur help!!!

Hi Jen

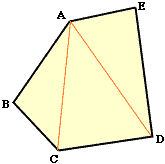
I am going to assume that the polygons you want to consider have each of their interior angles less than 180 degrees (we call such polygons convex). You need to know how to calculate the sum of the interior angles of any pentagon. Call the pentagon ABCDE.

  Choose a vertex (e.g. A) and draw all the diagonals possible from that point (AC & AD). You have now formed 3 triangles (ABC, ACD & ADE). Notice that the 9 angles in these 3 triangles (3 in each) will combine to form the 5 original angles. (e.g. <CAB + <DAC + <EAD = <EAB). So the sum of the 5 original angles is the same as the sum of the 9 angles in the 3 triangles. But the sum of the interior angles in a triangle is 180 degrees, so the sum of the 9 angles is 540 deg. Now you can do the original problem.
   Remember that a regular polygon has equal angles and equal sides. To find the size of each interior angle you subtract the measure of the exterior angle from 180 deg since the interior and exterior angle together form a straight angle. Remember that in a polygon of 5 sides you could make 2 diagonals and form 3 non-overlapping triangles and so the sum of the angles was (5 - 2)*180 deg. If the polygon has 4 sides you can make 1 diagonal and form 2 triangles. If it has 6 sides you can make 3 diagonals and form 4 triangles. It seems that in a polygon of n side you can make n - 3 diagonals and form n - 2 triangles. This makes sense because, to make a diagonal, you don't join the point to itself or to either of its immediate neighbours. So you can make n - 3 diagonals. This means that you have one more triangle: n - 2 triangles.
     So in a polygon of n sides the interior angles have a sum of (n - 2)*180 deg which is 180n - 360. But each of the n angles in a regular n-gon are equal and so the size of each angle is (180n - 360)/n. You know the size of your interior angle because you know the size of your exterior angle. So you set (180n - 360)/n = the size of the interior angle and solve the equation. If I were solving the equation, I would multiply both sides of the equation by n to clear the fractions.

Cheers,
Jack

Go to Math Central

To return to the previous page use your browser's back button.