Question:
In the puzzle called the Towers of Hanoi there are three peg and you are asked to move the rings from one peg and stack them in order on another peg. You can make as many moves as you want, but each move must consist of moving exactly one ring. Moreover, no ring may be placed on top of a smaller ring. The minimum number of moves required to move n rings is 1 for 1, 3 for 2 rings, 7 for 3 rings, 15 for 4 rings, and 31 for 5 rings. Find a formula for this sequence. What is the minimum number of moves required to move 6 rings?

Hi Jeni

This is a really nice problem so I don't want to tell you the answer. I will however give you a start.

Here is the situation with three rings on peg A and you are to move them to peg C.

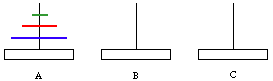
If you carefully perform the procedure to move the rings to peg C in seven steps you will see that you first moved the top two pegs (green and red) to peg B, then moved the blue ring to peg C and finally moved the green and red rings to peg C. Moving the green and red rings to peg B took 3 steps (3 moves for 2 rings), moving the blue ring to peg C took 1 step and moving the green and red rings to peg C took 3 steps (3 moves for 2 rings). This gives a total of 3 + 1 + 3 = 7 steps.
   See if you can use a similar argument to show that the procedure takes 15 steps for 4 rings and then 31 steps for 5 rings anf finally ??? steps for 6 rings.

Cheers,
Penny