Someone proposed this question to me and I do not know the answer, so I was wondering if you could help. How, using Roman Numeral, did people add, subtract, multiply, and divide with no zero or negative numbers?

Thanks in advance
Michelle Math 8

Hi Michelle

The best reference that I know on arithmetic with Roman Numerals is

Arithmetic with Roman Numerals, James G. Kennedy, American Math. Monthly 88:1 (Jan. 1981) 29-32.

What follows is extracted from Math 101 Online which is a course taught at the University of Regina.

A nice example of a number system other than our base 10 system that involves different symbols and incorporates different base arithmetic is the Roman system. The symbols used are:

Further intricacies of the system are the way in which the Roman numbers are written using combinations of these symbols. The numbers 1, 2, and 3 are simply I, II, III but for 4, rather than use IIII, the symbol IV is typically used, the I preceding the V denoting subtraction. Similarly we use IX for 9, XC for 90, etc. while XI and CX represent 11 and 110 respectively. For example, 1999 may be written as MDCCCCLXXXXVIIII, or, in shorter form, as MCMXCIX.
   How would we add or multiply in this system? Write the numbers without using the convention in the previous paragraph then the same basic ideas that we use in other bases apply -- we will take a column for I's, V's, X's, L's, C's, etc. The nature of the Roman system incorporates both base 2 and base 5 arithmetic -- we only need 2 V's to make an X, 2 L's to make a C, etc., but we need 5 I's to make a V, 5 X's to make an L, and so on. Thus,

         M  D   CC  L   XXX  V    II
            D  CCC       XX     IIII   
      +         CC  L   XXX  V    II
        MM  D  CCC  L  XXXX  V   III

In our base ten place value system:

        1787
         824  
      +  287
        2898

Similarly for a simple multiplication:

               CC  L  XXX  V  II
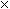                       X      I  
               CC  L  XXX  V  II
       MM  D  CCC  L   XX       
      MMM       C  L       V  II

which corresponds, in base 10, to 287 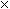11 = 3157, and a bit more complicated (and not so much fun),

                  CC  L  XXX  V   II
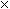                         XX     III  
                  CC  L  XXX  V   II
                  CC  L  XXX  V   II
                  CC  L  XXX  V   II
          MM  D  CCC  L   XX
          MM  D  CCC  L   XX              
      MMMMMM  D    C               I

i.e. 287 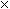23 = 6601.

Cheers
Penny