Subject: modular arithmetic
Name: Leslie
Who is asking: Student
Level: All
Question:
I am trying to do a project on modular arithmetic.
I was wondering if there were any websites that
include a sample lesson plan on modular arithmetic
for any grade level. Let me know where and how to
find them. Thanks.
Hi Leslie
What follows is a section from an online course that is offered at the University of Regina. It is not lesson plans but perhaps it will give you some ideas.
Harley
Arithmetic and Numeration Systems
Modular Arithmetic
- counting in hours - if it is 10:00 a.m. what time will it be 30 hours from now?
- counting in days - if it is Wednesday what day will it be 452 days from now?
- counting degrees - if you are facing north and spin clockwise 810 degrees, which way are you facing?
The idea that we need to use in these problems is counting in multiples -- of 12's, 7's, and 360's. In the first case we are only interested in the fact that 30 is 6 more than 24 and that 10 (a.m.) plus 6 leaves a remainder of 4 when we take away 12; in the second case that 452 leaves a remainder of 4 when we take away multiples of 7; 810 leaves a remainder of 90 when we take away multiples of 360. Thus we have as solutions: 4 p.m., Sunday and East.
In a more formal manner we say that (for integers a, b and m) that a is congruent to b modulo m if a and b leave the same remainder when divided by m. We usually denote this symbolically by a  b (mod m). This idea of congruence was first developed by the mathematician Carl Friedrich Gauss in the late 18th century. In our examples above we have 30
b (mod m). This idea of congruence was first developed by the mathematician Carl Friedrich Gauss in the late 18th century. In our examples above we have 30  6 (mod 12); 452
6 (mod 12); 452  4 (mod 7); 810
4 (mod 7); 810  90 (mod 360).
90 (mod 360).
Equivalent ways of stating the relationship of congruence include:
- a leaves a remainder of b when divided by m
For example: 10 4(mod 6), because 10
4(mod 6), because 10 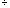 6 has a remainder of 4.
6 has a remainder of 4.
- a - b
 0 (mod m) i.e. a - b is a multiple of m
0 (mod m) i.e. a - b is a multiple of m
For example: 10 -2(mod 6), because 10 -(-2) = 12, which is a multiple of 6, and multiples of 6 have no remainders when divided by 6.
-2(mod 6), because 10 -(-2) = 12, which is a multiple of 6, and multiples of 6 have no remainders when divided by 6.
- a = tm + b for some integer t.
For example: 39 4(mod 7), because 39 = (5)(7) + 4.
4(mod 7), because 39 = (5)(7) + 4.
NOTE: Remember, with congruences we will be restricting ourselves to the integers.
More examples:
10  1 (mod 3); 1 (mod 3); | 5  -3 (mod 4); -3 (mod 4); | 1023  1 (mod 2); 1 (mod 2); |
1023  -1 (mod 2); -1 (mod 2); |
27  5 (mod 11); 5 (mod 11); | -18  4 (mod 7) 4 (mod 7) |
Exercises
1. 83  __ (mod 2) __ (mod 2) | 4. 78  __ (mod 7) __ (mod 7) | 7. 15  __ (mod 6) __ (mod 6) |
2. 23  __ (mod 5) __ (mod 5) | 5. 95  __ (mod 11) __ (mod 11) | 8. 81  __ (mod 9) __ (mod 9) |
3. 26  __ (mod 12) __ (mod 12) | 6. 16  __ (mod 2) __ (mod 2) | 9. 30  __ (mod 8) __ (mod 8) |
Addition and Multiplication
When we do modular arithmetic we throw away multiples of the modulus. Thus for example if we add 23 and 14 modulo 5 we end up with 37 modulo 5 which is 2 modulo 5; briefly 23 + 14 = 37  2 (mod 5). Similarly 16
2 (mod 5). Similarly 16 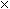 29 = 464
29 = 464  2 (mod 3). We can shorten our work sometimes by reducing the terms that we are working with by the modulus, thus
23 + 14
2 (mod 3). We can shorten our work sometimes by reducing the terms that we are working with by the modulus, thus
23 + 14  3 + 4 = 7
3 + 4 = 7  2 (mod 5), and 16
2 (mod 5), and 16 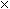 29
29  1
1 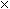 2 = 2 (mod 3). The salient point here is that we can throw away multiples of the modulus m before the arithmetic operation if we wish.
2 = 2 (mod 3). The salient point here is that we can throw away multiples of the modulus m before the arithmetic operation if we wish.
Let's look at addition and multiplication modulo 5. We arrange the results in tables as follows:
| + | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| 0 | 0 | 1 | 2 | 3 | 4 |
| 1 | 1 | 2 | 3 | 4 | 0 |
| 2 | 2 | 3 | 4 | 0 | 1 |
| 3 | 3 | 4 | 0 | 1 | 2 |
| 4 | 4 | 0 | 1 | 2 | 3 |
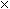 | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 2 | 3 | 4 |
| 2 | 0 | 2 | 4 | 1 | 3 |
| 3 | 0 | 3 | 1 | 4 | 2 |
| 4 | 0 | 4 | 3 | 2 | 1 |
For modulo 6 we have:
| + | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 2 | 3 | 4 | 5 |
| 1 | 1 | 2 | 3 | 4 | 5 | 0 |
| 2 | 2 | 3 | 4 | 5 | 0 | 1 |
| 3 | 3 | 4 | 5 | 0 | 1 | 2 |
| 4 | 4 | 5 | 0 | 1 | 2 | 1 |
| 5 | 5 | 0 | 1 | 2 | 3 | 4 |
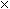 | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 2 | 3 | 4 | 5 |
| 2 | 0 | 2 | 4 | 0 | 2 | 4 |
| 3 | 0 | 3 | 0 | 3 | 0 | 3 |
| 4 | 0 | 4 | 2 | 0 | 4 | 2 |
| 5 | 0 | 5 | 4 | 3 | 2 | 1 |
Note that in modular arithmetic we can have a times b is 0 even when a and b are both non-zero, for example in (mod 6), 3 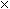 2
2  0 (mod 6), quite different from our usual arithmetic!
0 (mod 6), quite different from our usual arithmetic!
We can deal with equations in modular arithmetic in a manner very similar to that which we are used to in ordinary arithmetic. For example, solve 3z + 2  4 (mod 7) asks which integer(s) satisfy the congruence. Before we solve this problem we should observe that the equation 3z - 2 = 7 has the single solution of z = 3. When we deal with congruences many solutions, possibly infinitely many, may occur. Why is this? Well, consider 3z + 2
4 (mod 7) asks which integer(s) satisfy the congruence. Before we solve this problem we should observe that the equation 3z - 2 = 7 has the single solution of z = 3. When we deal with congruences many solutions, possibly infinitely many, may occur. Why is this? Well, consider 3z + 2  4 (mod 7) or 3z - 2
4 (mod 7) or 3z - 2  0 (mod 7). z = 3 is a solution since 3
0 (mod 7). z = 3 is a solution since 3 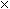 3 - 2 = 7
3 - 2 = 7  0 (mod 7) but notice also that 10 also works for 3
0 (mod 7) but notice also that 10 also works for 3 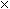 10 - 2 = 28
10 - 2 = 28  0 (mod 7). In fact once we have found the solution of z = 3 we have infinitely many solutions {3, 3 ± 7, 3 ± 2
0 (mod 7). In fact once we have found the solution of z = 3 we have infinitely many solutions {3, 3 ± 7, 3 ± 2 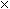 7, 3 ± 3
7, 3 ± 3 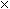 7, 3 ± 4
7, 3 ± 4 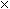 7, ..., 3 ± t
7, ..., 3 ± t 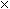 7, ... } (which is the same as the set of number {..., -25, -18, -11, -4 , 3, 10, 17, 24, ...}) since adding (or subtracting) multiples of 7 to our solution gives new solutions modulo 7: for example 3
7, ... } (which is the same as the set of number {..., -25, -18, -11, -4 , 3, 10, 17, 24, ...}) since adding (or subtracting) multiples of 7 to our solution gives new solutions modulo 7: for example 3 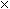 ( 3 + 52
( 3 + 52 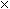 7) - 2
7) - 2  3
3 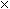 3 - 2 = 7
3 - 2 = 7  0 (mod 7). An important idea is buried in all of this -- when solving congruences we need only find one solution to find them all! We simply then add multiples of the modulus to find other solutions. Even more, this allows us to restrict our search, in the mod 7 case, for the first solution to the number 0, 1, 2, ..., 6.
0 (mod 7). An important idea is buried in all of this -- when solving congruences we need only find one solution to find them all! We simply then add multiples of the modulus to find other solutions. Even more, this allows us to restrict our search, in the mod 7 case, for the first solution to the number 0, 1, 2, ..., 6.
Examples:
Solve 4z + 1  2 (mod 9).
2 (mod 9).
Let's rewrite this as solve 4z - 1  0 (mod 9). Now try z = 0, 1, 2, ..., 8: for these values of z we have that 4z - 1 = -1, 3, 7, 11, 15, 19, 23, 27, 31 respectively; of these we want only multiples of 9, namely when z = 7, thus Solve 4z + 1
0 (mod 9). Now try z = 0, 1, 2, ..., 8: for these values of z we have that 4z - 1 = -1, 3, 7, 11, 15, 19, 23, 27, 31 respectively; of these we want only multiples of 9, namely when z = 7, thus Solve 4z + 1  2 (mod 9) has as solutions the set of numbers {7, 7 ± 9, 7 ± 18, 7 ± 27,...} = {..., -20, -11, -2, 7, 16, 25, 34,...}.
2 (mod 9) has as solutions the set of numbers {7, 7 ± 9, 7 ± 18, 7 ± 27,...} = {..., -20, -11, -2, 7, 16, 25, 34,...}.
Solve 5z - 1  3 (mod 8).
3 (mod 8).
Let's rewrite this as solve 5z - 4  0 (mod 8). Now try z = 0, 1, 2, ..., 7: for these values of z we have that 5z - 4 = -4, 1, 6, 11, 16, 21, 26, 31; we see that we want z = 4, thus solve 5z - 1
0 (mod 8). Now try z = 0, 1, 2, ..., 7: for these values of z we have that 5z - 4 = -4, 1, 6, 11, 16, 21, 26, 31; we see that we want z = 4, thus solve 5z - 1  3 (mod 8) has solutions, {4, 4 ± 8, 4 ± 16,...} = {..., -12, -4, 4, 12, 20,...}.
3 (mod 8) has solutions, {4, 4 ± 8, 4 ± 16,...} = {..., -12, -4, 4, 12, 20,...}.
Solve 2z  1 (mod 4), equivalently, 2z - 1
1 (mod 4), equivalently, 2z - 1  0 (mod 4).
0 (mod 4).
We try z = 0, 1, 2, 3, and find 2z - 1 = -1, 1, 3, 5, none of which are multiples of 4 so 2z  1 (mod 4) has no solutions. In other words, 2z - 1 can not be congruent to 0 (mod 4).
1 (mod 4) has no solutions. In other words, 2z - 1 can not be congruent to 0 (mod 4).
Exercises
- Construct the addition and multiplication tables for mod 7 arithmetic.
- Find the smallest positive solution to
2. 3456  x (mod 11)
x (mod 11)3. 823 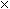 234
234  z (mod 8)
z (mod 8) - Find all solutions, if any, to
4. 7x  3 (mod 11)
3 (mod 11)5. 4z  1 (mod 6)
1 (mod 6)
To return to the previous page use your browser's back button.