Name: nicholas
Who is asking: Student
Level: Secondary

Question:
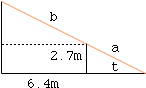
A vertical wall, 2.7m high, runs parallel to the wall of a house and is at a horizontal distance of 6.4m from the house. An extending ladder is placed to rest on the top B of the wall with one end C against the house and the other end, A, resting on horizontal ground. The points A, B, and C are in a vertical plane at right angles to the wall and the ladder makes an angle@, where 0<@<pye/2, with the horizontal. Show that the length, y metres, of the ladder is given by y= 2.7/sin@+6.4/cos@ As @ varies find the value of tan@ for which y is a minimum. Hence find the minimum value of y.

Hi Nicholas,

I drew a diagram, labeled the angle t and let a be the length of the part of the ladder from the ground to the wall and b the length of the rest of the ladder. From the diagram sin t = 2.7/a and cos t = 6.4/b. Thus a = 2.7/sin t and b = 64./cos t and hence the length of the ladder is y(t) = 2.7/sin t + 64./cos t  meters.    To find the minimum length of the ladder you need to differentiate y(t). Rather than work with fractions I would write y(t) = 2.7 csc t + 6.4 sec t and differentiate this form. After differentiating write all the trig fuctions in terms of sine and cosine before solving y'(t) = 0. I hope this helps, Harley