Subject: triangular and prime numbers

Hi Matt, The investigation of triangular numbers probably originated with the Pythagoreans. This was a school founded in the 6th century BC, composed of the followers of Pythagoras. Theirs was a secret society, so today nobody knows exactly what they studied and how it operated. Generally speaking, "figurate numbers" are the number of dots making up regular polygons as shown in the figures.

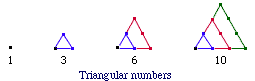
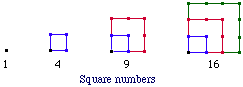
Triangular numbers and square numbers are the most common. The former make up the familiar sequence 1, 1+2=3, 1+2+3 = 6, ... . The general formula is

1+2+3+...+n = n(n+1)/2.

   In words, triangular numbers are those counting numbers that can be written n(n+1)/2 for some n. These numbers probably have been studied since the beginning of time, and their remarkable properties continue to fascinate mathematicians. For example, two hundred years ago the famous mathematician C.F. Gauss discovered (in 1796 at age 18) that every counting number is the sum of three triangular numbers (allowing 0 as a triangular number). So, for example, 10 = 1+3+6 = 0+0+10, and 11 = 0+1+10.

   Further details can be found in any elementary treatment of number theory. We took our information from AN INTRODUCTION TO THE HISTORY OF MATHEMATICS by Howard Eves.

Cheers,
Chris