Hi I am a 30 yo mature age student doing my HSC but am having difficulty understanding this, if you can help me.

From an airport control tower, a Cessna bears 023 degrees T and is 27km away. At the same time, a Boeing 767 bears 051 degrees T and is 61km from the tower. Both planes are at the same height.

i) What is the size of angle ATB?

ii) Using the cosine rule to calculate the distance the planes are apart, to nearest kilometre.

I figured out and drew the triangular diagram but can't figure out the rest and which formula to use. sorry about this, thankyou kindly

Hi Pammy,

This is my diagram. The tower is at T, N is north, the Cessna is at P and the Boeing 767 is at Q. Hence the angle PTN is 023 degrees and the angle QTN is 051 degrees. Thus the angle QTP is 51 - 23 = 28 degrees. What you have now is the triangle QTP, you know the lengths of two of the sides, you know the angle between these sides and you want the length of the third side. This is exactly what the Law of Cosines will find for you.

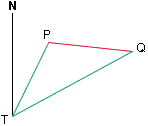
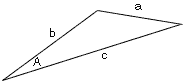
The Law of Cosines is usually stated with reference to the second diagram. The letters a, b and c designate the lengths of the three sides of a triangle and A is the angle opposite the side of length a. The Law of Cosines then says that a2 = b2 + c2 - 2 bc cos A For your problem b = 27 km, c = 61 km and A = 28 degrees. Thus |PQ|2 = 272 + 612 - 2(27)(61) cos(28)

Cheers
Harley