My age is 16, and my name is Richard. My question relates to the topic complex numbers & the quadratic formula.

I would like to know how to solve quadratic equations in which the discriminant is less than 0 (i.e. we get two complex solutions to the quadratic)

3x^2+2x+5 = 0

and how mathematicians like euler contributed to this field. If it would be possible I would also like to know how this type of quadratic equations can be graphed?

Thank you very much for your help and time

Your sincerely
Richard Peter

Hi Richard
It is exactly this type of problem that led mathematicians to introduce complex numbers and the symbol i for a number that satisfies z^2 = -1. There actually are two such numbers, the other is -i. A complex number z is then any number that can be written z = a + ib, where a and b are real numbers. a is called the real part of z and b the imaginary part of z. Looking at your equation, 3x^2+2x+5 = 0 the general quadratic gives

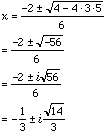
Thus 3x^2+2x+5 = 0 has two solutions,

   Euler was the first mathematician to use the letter i to denote this complex number. You can find a historical note on the symbol i at Earliest Uses of Various Mathematical Symbols
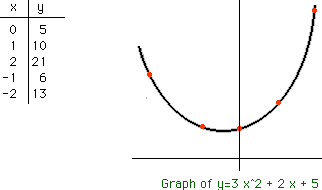
   Quadratic equations with a negative discriminant are graphed as any other quadratic equation. What you will notice is that they do not cross the x-axis. For your example y=3x^2+2x+5 we know that there are no points on the graph with y=0 since the only solutions to y=0 are

If you plot some points you can sketch the graph of y=3x^2+2x+5.

Cheers
Harley