I am a teacher of secondary mathematics with a question about the uses of Three Dimensional Co-ordinate Geometry. I have been teaching my students to write equations of planes and lines, - to find the intersection of these and the distance between them. What I am having difficulty finding are good applications of these techniques to "real world" situations. Can anybody help me?
Thanks for consideration of this problem,

Sincerely
Dave

Hi Dave,
The process of converting from plane equations to lines, points, distances etc. is central to a lot of work in computer graphics, animation, robotic vision and computational geometry in general.

Consider a few examples:

	Take four planes and find the vertices, edges and volume of the tetrahedron they describe.
	Do the same with six planes that describe an open top box (the top plane is transparent). To place an image of this box on a computer or TV screen as seen from some point (eye) in three space, draw a line from the eye to each point on the screen. For each line decide which of the five non-transparent sides of the box the line hits first. That is what you see on the screen, the rest of the box is hidden.    Now find a way to do it fast as I want the box to tumble through three space and watch the image on the screen.
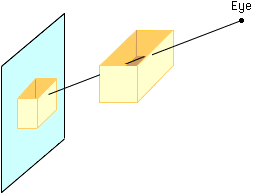
	Take three intersecting planes in 3-space. Consider the picture viewed down the z-axis: For each point in the picture, which plane is in view (on top) and which is hidden. Where are the boundaries in this picture (the lines of intersection)?    Now what should I do if the picture is not three planes but, say 100 planes? what is the process for drawing a view of the object? Which processes are 'fast'? which are 'slow'?

Pieces like the previous example occur inside linear programming, but with analogs of planes in say, 1000 dimensions, still looking for vertices and edges to walk along in the search for a 'top' point in a 'view'.

Hope this helps.
Walter Whiteley and Harley